K-means Clustering

Haz tu propio algoritmo de clusterización de datos de tipo K-means (o mediante K-means). No te preocupes si no sabes cómo es el algoritmo, te lo vamos qué pasos debes dar con pseudo-código.

Los datos de entrada para clusterizar

Haremos uso de la librería Scikit-learn -de la cual hablaremos más extensamente la semana que viene- para generar un conjunto de datos que clusterizar:

from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np

dataset, membership = datasets.make_blobs(n_samples=500, n_features=2,
                                          centers=3, cluster_std=1.0)

La variable dataset contiene un numpy.array con 500 puntos en un espacio bidimensional:

dataset.shape

(500, 2)

La variable membership nos da la solución al problema que pretendemos resolver… nos dice a qué cluster pertenece cada punto según contenga un 0, 1 o 2:

membership

array([1, 1, 0, 1, 2, 1, 1, 2, 0, 1, 2, 2, 0, 2, 2, 2, 2, 2, 0, 0, 0, 2,
       1, 0, 0, 0, 1, 2, 1, 2, 2, 1, 1, 2, 0, 2, 1, 1, 2, 2, 2, 0, 2, 1,
       2, 0, 1, 2, 2, 1, 1, 2, 2, 0, 0, 0, 0, 1, 0, 2, 2, 0, 1, 0, 0, 0,
       2, 1, 0, 0, 1, 0, 1, 2, 0, 2, 2, 0, 1, 1, 2, 0, 1, 1, 0, 1, 0, 2,
       2, 2, 0, 0, 2, 1, 2, 0, 0, 1, 0, 2, 0, 0, 2, 2, 1, 0, 1, 1, 0, 1,
       0, 1, 2, 0, 2, 2, 1, 1, 0, 0, 1, 0, 1, 0, 1, 2, 0, 2, 2, 1, 1, 2,
       2, 2, 2, 1, 1, 1, 2, 1, 1, 2, 0, 1, 2, 0, 0, 0, 2, 2, 0, 0, 2, 0,
       1, 1, 1, 2, 2, 0, 2, 0, 0, 1, 0, 1, 1, 2, 0, 0, 1, 2, 0, 2, 1, 2,
       2, 2, 0, 2, 0, 2, 2, 0, 1, 1, 0, 2, 2, 0, 1, 1, 0, 0, 2, 1, 0, 0,
       1, 0, 1, 1, 1, 2, 0, 2, 2, 1, 0, 1, 2, 1, 0, 1, 2, 0, 0, 0, 1, 2,
       1, 1, 2, 2, 0, 0, 2, 0, 1, 2, 2, 1, 0, 1, 0, 1, 2, 0, 1, 0, 0, 0,
       2, 2, 0, 0, 0, 1, 0, 1, 0, 2, 2, 2, 1, 1, 0, 2, 2, 0, 1, 0, 1, 0,
       0, 2, 1, 1, 0, 2, 2, 1, 1, 2, 2, 0, 1, 1, 0, 2, 1, 1, 0, 0, 0, 1,
       1, 0, 0, 2, 2, 2, 1, 2, 0, 0, 2, 2, 1, 0, 1, 0, 1, 0, 2, 0, 0, 1,
       0, 0, 2, 1, 2, 2, 0, 1, 2, 2, 2, 1, 0, 1, 2, 0, 0, 2, 1, 0, 1, 2,
       2, 2, 0, 0, 0, 2, 2, 1, 1, 1, 1, 2, 2, 1, 2, 2, 2, 1, 1, 1, 2, 2,
       0, 1, 1, 0, 2, 0, 2, 2, 2, 2, 1, 2, 0, 2, 2, 2, 0, 0, 0, 0, 1, 2,
       1, 0, 0, 1, 0, 1, 1, 0, 2, 1, 0, 1, 0, 1, 0, 2, 0, 2, 1, 0, 2, 0,
       0, 0, 1, 2, 2, 2, 0, 0, 2, 0, 2, 1, 2, 0, 0, 0, 1, 1, 2, 0, 1, 1,
       0, 1, 0, 2, 2, 0, 1, 0, 1, 1, 1, 2, 1, 0, 2, 0, 1, 2, 0, 1, 0, 1,
       1, 2, 1, 2, 2, 1, 1, 0, 2, 1, 1, 2, 2, 2, 2, 1, 0, 1, 2, 0, 0, 0,
       1, 1, 0, 0, 0, 1, 1, 1, 1, 2, 1, 2, 0, 0, 1, 1, 2, 1, 2, 1, 2, 2,
       1, 1, 0, 2, 1, 2, 1, 1, 1, 1, 1, 1, 2, 0, 0, 1])

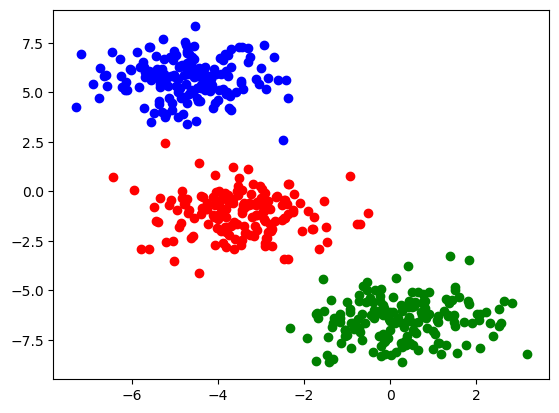
Usemos dataset y membership para representar gráficamente los puntos que usaremos como «datos a clusterizar». Vamos a colorear cada punto de un color según a que cluster pertenecen:

plt.scatter(dataset[(membership==0),0], dataset[(membership==0),1], color='r')
plt.scatter(dataset[(membership==1),0], dataset[(membership==1),1], color='g')
plt.scatter(dataset[(membership==2),0], dataset[(membership==2),1], color='b')
plt.show()

Haz tu propio algoritmo K-means

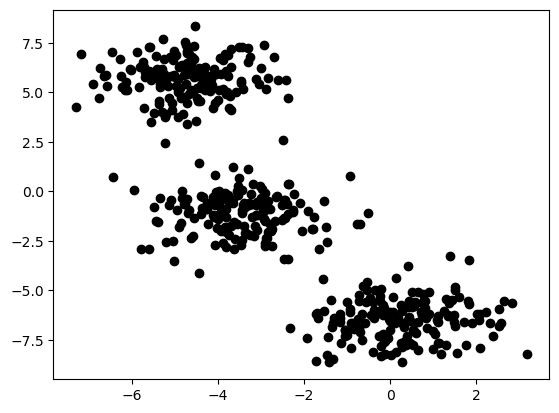
Supon que tienes almacenados en una variable llamada dataset un numpy.array con las coordenadas \(x\) e \(y\) de 500 puntos:

plt.scatter(dataset[:,0], dataset[:,1], color='k')
plt.show()

Y quieres clusterizar los datos en 3 conjuntos de puntos con un algoritmo de K-means, pero no tienes acceso a ninguna librería de Python que tenga una función para hacerlo… Así que… tendrás que implementar tu propia función de K-means clustering.

A continuación tienes la descripción del algoritmo en pseudo código. Implementa tu propio algoritmo y representa gráficamente la distribución de puntos de dataset en el espacio bidimensional con un color distinto según al cluster que pertenecen resultado de tu algoritmo. ¿Puedes reproducir la primera gráfica de este notebook?

Pseudo-código del algoritmo de K-means

1. Elije el número de k centroides (en nuestro caso k=3)

2. Inicializa de forma aleatoria las coordinadas de los k centroides en el espacio de coordenadas de tus datos. Estos k centroides pueden ser puntos nuevos con coordenadas aleatorias, o pueden ser k puntos de tu dataset elegidos al azar.

3. Itera:

4.   Asigna cada punto de tu dataset al centroid más cercano.
   

5.   Calcular las nuevas coordenadas de los k centroides como el centro geométrico del conjunto >de puntos que le fueron asignados en 4.
   

6.   Calcula la distancia euclidea que se desplazó cada centroide.
   

7.   Sal de la iteración si las coordenadas de los centroides no cambiaron (si todos los desplazamientos calculados en 6 son prácticamente nulos).
   

8. Identifica los k cluster resultantes como los k conjuntos de puntos de tu data set asignados a cada centroide.

### ES TU TURNO
### -----------------------------------
### Resuelve aquí la propuesta anterior
### en una o varias celdas