Cálculo del número Pi por un método MonteCarlo

Si lanzamos un par de números aleatorios, \(x\) y \(y\), cuya densidad de probabilidad es uniforme en el segmento del plano XY definido por \([0,1)x[0,1)\). ¿Cúal será la probabilidad de que este punto \((x,y)\) se encuentre a una distancia menor o igual que \(1\) del punto \((0,0)\)? ¿Qué número irracional encontraremos como el cuadruple de dicha probabilidad?

Tarea

Dada una secuencia de \(N\) pares de números aleatorios (\(x\),\(y\)) donde \(0<=x<1\) y \(0<=y<1\), calcula la probabilidad que tuvo cualquiera de sus puntos (\(x\),\(y\)) de encontrarse a una distancia menor o igual que \(1\). Esa probabilidad será el número de puntos \(q\) que cumplen esa condición dividido \(N\):

(1)\[\begin{equation} P= \frac{q}{N} \end{equation}\]

Veamos como generar con Numpy por ejemplo 100 puntos (\(x\),\(y\)) en el espacio bidimensional definido por \([0,1)x[0,1)\):

import numpy as np

puntos = np.random.rand(10000,2)

¿Podrías representar gráficamente con ayuda de la librería MatPlotLib estos puntos en el espacio? ¿Sabrías representar en color rojo los puntos que se encuentran a una distancia menor que 1 del punto (0,0) y en azul el resto?

from matplotlib import pyplot as plt

dentro=[]
fuera=[]

for x,y in puntos:
    if (x**2+y**2)<=1.0:
        dentro.append([x,y])
    else:
        fuera.append([x,y])

dentro=np.array(dentro)
fuera=np.array(fuera)

plt.scatter(dentro[:,0], dentro[:,1], c='r', s=0.2)
plt.scatter(fuera[:,0], fuera[:,1], c='b', s=0.2)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
ax = plt.gca()
ax.set_aspect('equal')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

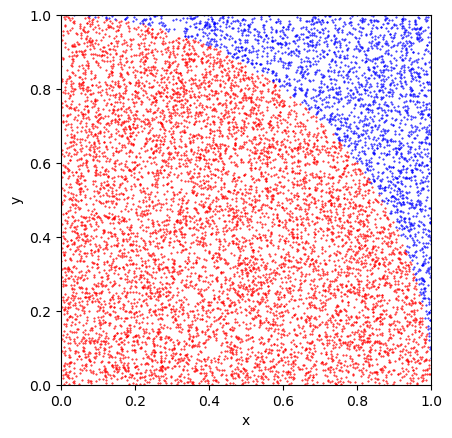
Habrás visto que los puntos rojos se encuentran en una zona de área igual a un cuarto de un círculo de radio 1. Podrás entonces calcular la probabilidad teórica de que un punto cumpla la condición de estar a una distancia menor o igual que 1 del punto (0,0) como el área del cuarto de círculo de radio 1 dividido por el área del cuadrado de lado 1:

(2)\[\begin{equation} P= \frac{\pi}{4} \end{equation}\]

De esta manera podemos calcular \(\pi\) de la probabilidad de que un punto aleatorio se encuentre a una distancia menor o igual que 1 de (0,0):

(3)\[\begin{equation} \pi= 4\cdot \frac{q}{N} \end{equation}\]

¿Qué valor de \(\pi\) obtienes con 100 números aleatorios?

N=100
puntos = np.random.rand(N,2)

q=0
for x,y in puntos:
    if (x**2+y**2)<=1.0:
        q+=1

print(f'El valor de pi obtenido con 100 números aleatorios es: {4*q/N}')

El valor de pi obtenido con 100 números aleatorios es: 3.12

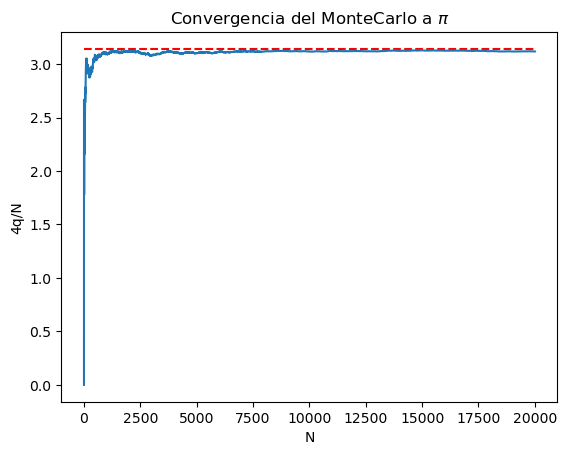
Por último, representa gráficamente el valor que obtienes de \(\pi\) frente a \(N\) cuando \(N\) toma valores entre 1 y un número suficientemente largo como para observar la convergencia del valor calculado de \(4\cdot \frac{q}{N}\) al número irracional que conocemos como \(\pi\):

N=20000
puntos = np.random.rand(N,2)

pi_list = []
N_list = []

ii=1
q=0
for x,y in puntos:
    if (x**2+y**2)<=1.0:
        q+=1
    pi_list.append(4*q/ii)
    N_list.append(ii)
    ii+=1

plt.hlines(3.14159265359, 0.0, N, linestyles='--', color='r')
plt.plot(N_list, pi_list)
plt.xlabel('N')
plt.ylabel('4q/N')
plt.title(r'Convergencia del MonteCarlo a $\pi$')
plt.show()